S-双対
理論物理学では、S-双対(S-duality)は、2つの物理理論の等価のことで、この物理理論は場の量子論でも弦理論でもよい。S-双対は、計算することが難しい理論をより計算し易い理論に結びつけるので、理論物理で計算する際に有益である。[1]
場の量子論では、S-双対性は、古典電磁気学で良く知られた事実、すなわち、電場と磁場の交換の下にマクスウェルの方程式の不変であると言う事実を一般化したものである。場の量子論で最も早く知られたS-双対の例の一つは、モントネン・オリーブの双対性(Montonen-Olive duality)で、N=4 超対称ヤン・ミルズ理論と呼ばれる場の量子論の 2つのバージョンを関係付けている。アントン・カプスティン(Anton Kapustin)とエドワード・ウィッテン(Edward Witten)の最近の仕事は、モントネン・オリーブの双対性が幾何学的ラングランズ対応と呼ばれる数学の研究プログラムと密接に関係していることを示している。[2] 場の量子論でのもう一つのS-双対の実例は、サイバーグ双対(Seiberg duality)で、N=1超対称ヤン・ミルズ理論(N=1 supersymmetric Yang-Mills theory)と呼ばれる 2つのバージョンの理論を関連付ける。
弦理論には多くのS-双対の例がある。これらの弦双対性(string duality)の存在は、一見異なるように見える弦理論の定式化が、実際は物理的等価であることを意味する。このことは1990年代中期には全ての 5つの整合性をもった超弦理論の全てが、単一の 11次元のM-理論と呼ばれる理論の異なる極限として実現されることを導いた。[3]
オーバービュー
場の量子論や弦理論では、結合定数は理論の相互作用の強さを制御する数値である。例えば、重力の強さはニュートン定数と呼ばれる数値で書かれ、重力のニュートンの法則の中や、アルバート・アインシュタイン(Albert Einstein)の一般相対論の方程式の中にも表れる。同様に、電磁場の強さは、結合定数により表され、一つの陽子の帯びている電荷に関係している。
場の量子論や弦理論で観測可能量を計算するためには、物理学者は典型としては摂動論(perturbation theory)の方法を適用する。摂動論では、発生する様々な物理的な過程の確率を決定する確率振幅(probability amplitude)と呼ばれる量が、無限級数の和として表され、そこでは各々の項は結合定数 のべきと比例する。
- .
このようなべき級数展開が意味を持つためには、結合定数が 1 よりも小さい必要があり、従って の高い次数のべきは無視できるほどに小さく、和は有限となる。結合定数が 1 よりも大きいと、この項の和はどんどんと大きくなり、展開は意味のない無限大の値をもたらす。この場合、理論は「強い結合」といわれ、摂動論を予言をすることに使うことができない。
ある理論に対して、S-双対は強い結合定数の理論での計算を弱い結合定数の理論での異なる計算に変換することで、計算を進める方法を提供する。S-双対は、物理学の双対性という一般的な考え方の特別な例である。双対性ということばは、2つの一見異なる物理系が非自明な方法で等価であることが分かることを意味する。2つの理論が双対関係にあると、一つの理論から何らかの方法でもう一つの理論のように見える結果へと変換できることを意味する。このときに、2つの理論はこの変換の下で互いに双対であるという。別な言い方をすると、2つの理論が同じ現象の数学的には異なる記述となっているとも言える。
S-双対は、結合定数 を持つ理論を、結合定数 を持つ等価な理論と関係付けるので、有益である。このように、S-双対は、強結合の理論(そこでは結合定数 が 1 よりも非常に大きい)を弱結合の理論(そこでは結合定数 が 1 よりも小さく、計算が可能)へと関連付ける。この理由から、S-双対は、強弱双対性と呼ばれる。
場の量子論でのS-双対
マクスウェル方程式の対称性
古典物理学では、電場と磁場の振る舞いはマクスウェル方程式として知られる一連の方程式で記述される。ベクトル解析の言葉では、電荷も電流もない空間の領域の中にいることを前提とすると、マックスウェル方程式は次のように書かれる。[4]
ここに は電場を表すベクトル(さらに詳しくは、ベクトル場で、値を空間内の異なる点では変化しうる)で、 は磁場を表すベクトルであり、 は時間、 は光速度である。これらの方程式で使われている他のシンボルは、ベクトル解析の中の勾配 (ベクトル解析)("grad"という記号)、発散 (ベクトル解析)("div"という記号)、回転 (ベクトル解析)("curl"という記号)を参照のこと。
これらの方程式[5]の重要な性質は、電場 を磁場 へ、磁場 を電場 へ同時に置き換える変換のしたで、不変であることである。
言い換えると、マクスウェル方程式の解くような電場と磁場が与えられると、これらの電場と磁場が入れ替えても、新しい場がマクスウェル方程式の解を再び与えるような新しい物理的な設定することが可能となる。
この状況が、場の量子論の中のS-双対の最も基本的な事項である。実際、以下に説明するように、場の量子論のフレームワークには、このマックスウェル方程式の対称性を直接一般化したS-双対のバージョンが存在する。
モントネン・オリーブ双対性
場の量子論では、電場と磁場は電磁場と呼ばれる一つの実在に統一されていて、この場はゲージ理論あるいは、ヤン=ミルズ理論と呼ばれる場の量子論の特別なタイプにより記述される。ゲージ理論では、物理場は高い対称性の度数を持っていて、数学的にはリー群の考えを使い理解することができる。このリー群はゲージ群として知られている。電磁場は、ゲージ群U(1)に対応する最も単純なゲージ理論により記述されるが、しかし他のより向く雑な非アーベル的ゲージ理論も存在する。[6]
マクスウェル方程式の中の対称に相互作用する電場と磁場のゲージ理論の類似物が存在するか否かを問うという 、自然な疑問がある。1970年代末にこの回答が、クラウス・モントネン(Claus Montonen)とダヴィッド・オリーブ[7] により与えられた。この仕事は、より早い段階ピーター・ゴダード (物理学者)(Peter Goddard)、ジャン・ヌイツ(Jean Nuyts)、オリーブによる仕事[8]の仕事に基づくものであった。彼らの仕事は、現在モントネン・オリーブの双対性として知られてるS-双対の例をもたらした。モントネン・オリーブの双対性は、N=4 超対称ヤン・ミルズ理論と呼ばれるゲージ理論の非常に特殊なタイプに適用され、このことは 2つのその理論が正確な意味で等価ではないかということを言っている。[1] 理論の一つがゲージ群 を持っていると、双対な理論はゲージ群 を持っている。ここに は一般には とは異なるラングランズ双対群を表している。[9]
場の量子論の重要な量は、複素化された結合定数である。これは次の公式により定義される複素数である。[10]
ここに、 はテータ角で、理論を定義するラグラジアンに現れる量であり[11]、 は結合定数である。例えば、電磁場を記述するヤン=ミルズ理論では、この数値 は単に陽子に帯びている電荷 である。[12] 2つの理論のゲージ群の入れ替えに加えて、モントネン・オリーブの双対性は、複素化された結合定数 を持つ理論を、複素化された結合定数 を持つ理論へ変換する。[10]
ラングランズプログラムとの関係
数学では、古典的なラングランズ対応は、数論を表現論として知られている数学の分野と関連される予想と結果の集まりである。[13] ロバート・ラングランズ(Robert Langlands)により1960年代遅くに、ラングランズ対応は谷山・志村予想というような数論の重要な予想と関連している。これは特別な場合としてフェルマーの最終定理を特別な場合として持っている。[13]
数論ではラングランズ対応は重要であるにも関わらず、数論の脈絡でのラングランズ対応の確立は非常に困難である。[13] 結果として、幾何学的ラングランズ対応として知られていることに関連する予想で仕事をしている数学者もいる。これは、元来のバージョンに現れる数体を函数体に置き換えることで、代数幾何学のテクニックを適用して、古典的なラングランズ対応を幾何学的に再定式化することである。[14]
2007年からのアントン・カプスティン(Anton Kapustin)とエドワード・ウィッテン(Edward Witten)は、幾何学的ラングランズ対応がモントネン・オリーブ双対性の数学的記述と見なすことができることを示した。[15] S-双対で関連付けられた 2つのヤン=ミルズ理論から始めて、カプスティンとウィッテンは、2次元時空内の場の量子論のペアを構成することが可能であることを示した。何がこの次元簡約(dimensional reduction)がD-ブレーン(en:D-branes)と呼ばれる物理的対象となるのかを分析することにより、彼らは幾何学的ラングランズ対応の数学的な要素を再現できることを示した。[16] かれらの仕事は、ラングランズ対応が場の量子論のS-双対に密接に関連していて、双方の対象に有効に適用できることを示した。[13]
サイバーグ双対性
もう一つ別の場の量子論でのS-双対の実例は、サイバーグ双対性であり、1995年頃に最初にナタン・サーバーグ(Nathan Seiberg)により導入された[17]。モントネン・オリーブ双対性とは異なり、4次元の時空での最大超対称性ゲージ理論の 2つのバージョンを関係付ける。サイバーグ双対性は、より小さな超対称性を持つN=1超対称性ゲージ理論(N=1 supersymmetric gauge theories)を関連付ける。サイバーグ双対性に現れる 2つの N=1 理論は、同一ではないが、長い距離では同じ物理を生成する。モントネン・オリーブ双対性のように、サイバーグ双対性は電場と磁場を入れ替えるマックスウェル方程式の対称性を一般したものである。
弦理論の中のS-双対
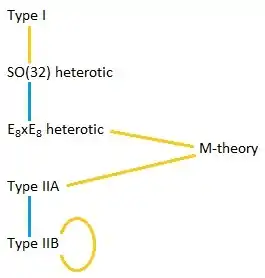
1990年代中期、弦理論の物理学者たちは、別々の理論のバージョンは 5つあると信じていた。すなわち、タイプ I, タイプ IIA、タイプ IIBと、2つのヘテロ弦理論(SO(32)のタイプとE8×E8のタイプ)である。異なるタイプの理論には異なるタイプの弦があり、低エネルギーでの粒子は異なる対称性を示す。
1990年代中期、物理学者たちは、これらの 5つの理論が実際は、高度に非自明な双対性で関連付けられていることに気がついた。これらの双対性のうちの一つがS-双対である。弦理論でのS-双対の存在は、最初は、1994年にアショク・セン(Ashoke Sen)によって提案された[18]。結合定数 を持つタイプ IIBの弦理論が、結合定数 を持つ自分自身のタイプ IIBの弦理論にS-双対(自己双対)を通して等価であることを示した。同様に、結合定数 を持つタイプ Iの弦理論は、結合定数 を持つ SO(32) のタイプのヘテロ弦理論と等価であることを示した。
それまでは、これらの双対性の存在は 5つの弦理論が実際はすべて異なる理論であったが、1995年の南カリフォルニア大学での弦理論のコンファレンスで、エドワード・ウィッテンはこれらすべての 5つの弦理論がM-理論として知られる単一の理論の異なる極限であるとう驚くべき示唆を行った[19]。ウィッテンの提案は、タイプ IIAとタイプ E8×E8 のヘテロ弦理論が密接に 11次元の超重力理論と呼ばれる重力理論に関係しているという見方を基礎としている。彼の発言は、第二超弦理論革命の最盛期を築き上げた。
関連項目
- T-双対
- U-双対
- ミラー対称性 (弦理論)
- AdS/CFT対応
脚注
- Frenkel 2009, p.2
- Kapustin and Witten 2007
- Zwiebach 2009, p.325
- Griffiths 1999, p.326
- Griffiths 1999, p.327
- ゲージ理論の基礎を含む一般の場の量子論の入門書として、Zee 2010を参照のこと。
- Montonen と Olive 1977
- Goddard, Nuyts, and Olive 1977
- Frenkel 2009, p.5
- Frenkel 2009, p.12
- Frenkel 2009, p.12
- Frenkel 2009, p.2
- Frenkel 2007
- Frenkel 2007
- Kapustin と Witten 2007
- Aspinwall et al. 2009, p.415
- Seiberg 1995
- Sen 1994
- Witten 1995
参考文献
- Aspinwall, Paul; Bridgeland, Tom; Craw, Alastair et al., eds (2009). Dirichlet Branes and Mirror Symmetry. American Mathematical Society. ISBN 978-0-8218-3848-8
- Frenkel, Edward (2007). “Lectures on the Langlands program and conformal field theory”. Frontiers in number theory, physics, and geometry II (Springer): 387–533. arXiv:hep-th/0512172. Bibcode: 2005hep.th...12172F.
- Frenkel, Edward (2009). “Gauge theory and Langlands duality”. Seminaire Bourbaki.
- Goddard, Peter; Nuyts, Jean; Olive, David (1977). “Gauge theories and magnetic charge”. Nuclear Physics B 125 (1): 1–28. Bibcode: 1977NuPhB.125....1G. doi:10.1016/0550-3213(77)90221-8.
- Griffiths, David (1999). Introduction to Electrodynamics. New Jersey: Prentice-Hall
- Kapustin, Anton; Witten, Edward (2007). “Electric-magnetic duality and the geometric Langlands program”. Communications in Number Theory and Physics 1 (1): 1–236. arXiv:hep-th/0604151. Bibcode: 2007CNTP....1....1K. doi:10.4310/cntp.2007.v1.n1.a1.
- Montonen, Claus; Olive, David (1977). “Magnetic monopoles as gauge particles?”. Physics Letters B 72 (1): 117–120. Bibcode: 1977PhLB...72..117M. doi:10.1016/0370-2693(77)90076-4.
- Seiberg, Nathan (1995). “Electric-magnetic duality in supersymmetric non-Abelian gauge theories”. Nuclear Physics B 435 (1): 129–146. arXiv:hep-th/9411149. Bibcode: 1995NuPhB.435..129S. doi:10.1016/0550-3213(94)00023-8.
- Sen, Ashoke (1994). “Strong-weak coupling duality in four-dimensional string theory”. International Journal of Modern Physics A 9 (21): 3707–3750. arXiv:hep-th/9402002. Bibcode: 1994IJMPA...9.3707S. doi:10.1142/S0217751X94001497.
- Witten, Edward (13–18 March 1995). "Some problems of strong and weak coupling". Proceedings of Strings '95: Future Perspectives in String Theory. World Scientific.
- Witten, Edward (1995). “String theory dynamics in various dimensions”. Nuclear Physics B 443 (1): 85–126. arXiv:hep-th/9503124. Bibcode: 1995NuPhB.443...85W. doi:10.1016/0550-3213(95)00158-O.
- Zee, Anthony (2010). Quantum Field Theory in a Nutshell (2nd ed.). Princeton University Press. ISBN 978-0-691-14034-6
- Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9